ARIMA를 통한 월간 전력수요 예측
전력수요예측은 전력가격예측에서 필수적인 요소이다. 다른 변수(발전소 건설계획, 유가)에 비해서는 상당히 안정적인 시계열을 가지고 있기 때문에, 비교적 쉽게 분석할 수 있다. 본글에서는 전력 젼력거래소 EPSIS의 전력수급현황에서 공개되는 1960년~2016년 월별 데이터를 토대로 분석을 해볼 것이다.
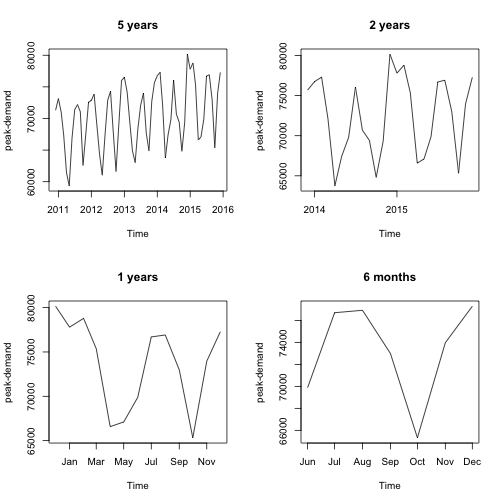
우선 전체적인 그림을 파악하기 위해서 최근 월간수요예측을 구간별로 나누어 보겠다. 아래의 그래프를 보면, 가장 눈에 띄는 것이 전력수요의 계절성(seasonality)이다. 여름/겨울에 많은 전기를 쓰고, 봄/가을에서는 상대적으로 적게쓴다. 3개월 주기에 따라서 Up&Down이 있다는 것을 알 수 있다.
ARIMA 모형
본 글에서는 자기이동회귀평균(ARIMA,Autoregressive integrated moving average) 방법을 통해서 전력수요를 시계열 예측해볼 것이다. 과거의 데이터의 가중합(AR:자기회귀)과 과거의 예측의 오차의 가중합(MA,이동평균) 혼합해서 예측하는 기법이다. 자기회귀이동평균은 원칙적으로 안정적(stationary)인 데이터에만 쓰인다. 불안정하지만, 일정한 패턴이 있는 시계열의 경우 차분(differentiation:Integration)을 통해서 시계열 예측을 한다.
ARIMA(p,d,q)(P,D,Q)N에서 (p,d,q)는 p는 자기회귀(AR)를 할 항의 개수, d는 차분계수(Integration), q는 이동평균(MA)의 개수를 의미한다. 또한 (P,D,Q)N는 계절성이 있는 ARIMA분석에서 쓰이는 계수이다. P는 계절AR계수, D는 계절차분, Q는 계절 이동평균을 의미한다. N은 계절계수를 의미한다. 월단위 자료인데, 1년단위로 계절성이 지속된다면, N=12 이다. ARIMA모델을 간단히 식으로 표현하면 아래와 같다.
\[ARIMA(p,d,q): Y_t=C(상수)+Y_{t-1}* \phi_{t-1}+\\ ...+Y_{t-p}* \phi_{t-p}+\epsilon_{t-1}* \theta_{t-1}+\\ ....\epsilon_{t-q}* \theta_{t-q} \\ 설명: \ C(상수):Y값의\ 평균 \,,\phi:AR계수 \ \\ ,\theta:MA계수, \epsilon:오차(백색잡음)\]ARIMA모델은 후방연산자(backshift operator)를 가지고 표현될 수도 있다.후방연산자(B)는 현재의 값을 기준으로 과거의 값을 구할수 있는 연산자이다. ARIMA모형을 단순화시키고, 백색잡음과 각하의 관계를 명확하게 설정한다. 후방연산자는 아래의 식을 만족한다.
\[후방연산자\;기본모형:B^nY_t=Y_{t-n} \\\]AR(p)의 경우 다음식으로 표현될 수 있다. 후방연산자를 통해서 백색잡음과 관계를 설정할 수 있다. 또한 $\Phi(B)$ 을 AR(p)의 특성함수라고 부른다.
\[Y_t=\Phi_1 Y_{t-1}+ \Phi_2 Y_{t-2}\; \dots+ \Phi_p Y_{t-p} + \epsilon_t \\ Y_t=\Phi_1BY_t+\Phi_2B^2Y_t+\; \dots+\Phi_pB^p Y_t + \epsilon_t\\ (1-\Phi_1B-\Phi_2B^2\dots-\Phi_pB^p))Y_t=\epsilon_t \\ \Phi(B)Y_t=\epsilon_t\]MA(q) 모형의 후방연산자는 $\theta(B)$ 는 MA(q)의 특성함수라고 부른다.
\[Y_t=\epsilon_t-\theta_{1}\epsilon_{t-1}-\theta_{2}\epsilon_{t-2}-\dots \theta_{q}\epsilon_{t-q}\\ Y_t=\epsilon_t-\theta_{1}B\epsilon_t-\theta_{2}B^2\epsilon_t-\dots \theta_{q}B^q\epsilon_t\\ Y_t=\epsilon_t(1-\theta_{1}B-\theta_{2}B^2-\dots \theta_{q}B^q)\\ Y_t=\epsilon_t\theta(B) \\\]만약에서 차분한 시계열일 경우 후방연산자는 아래와 같이 된다.\(\bigtriangledown(B)\)는 차분항의 특성함수라고 부른다.
\[1회\; 차분:y_t=Y_t-Y_{t-1}=Y_{t}-BY_t=(1-B)Y_t \\ 2회\; 차분: z_t=y_t-y_{t-1} \\ =(1-B)Y_t-(Y_{t-1}-Y_{t-2})\\ =(1-B)Y_t-BY_t-B^2Y_t\\ =(1-B)Y_t+B(1-B)Y_t\\ =(1+B)(1-B)Y_t\\ \vdots \\ n회 차분:a_t= (1+B)^{n-1}(1-B)Y_t\]ARIMA모형은 자기회귀(AR),차분(diffentiation/Integration), 이동평균(MA)을 조합해서 최적의 예측을 찾는 것이다. 그렇다면 각 식의 후방연산자와 이를 통해서 들어난 특성함수를 통해서 ARIMA모형을 단순화 시킬수 있다. 비정상적인 시계열 $Y_1 \dots Y_t$를 n회 차분한 시계열을 $y_t$라고 하자. 그렇다면 해당 시계열은 아래와 같이 표현될 수 있다.
\[y_t=\bigtriangledown^n Y_t\;(Y_t를\;n회\;차분한\;시계열)\\ y_t=\Phi_1 y_{t-1}+ \Phi_2 y_{t-2}\; \dots+ \Phi_p y_{t-p} + \\ \epsilon_t-\theta_{1}\epsilon_{t-1}-\theta_{2}\epsilon_{t-2}-\dots \theta_{q}\epsilon_{t-q}\\ \Phi(B)y_t=\epsilon_t\theta(B)\\ \bigtriangledown^nY_t=y_t=\frac{\theta(B)}{\Phi(B)} \epsilon_t\\ Y_t=\bigtriangledown(B)* \frac{\theta(B)}{\Phi(B)} \epsilon_t\]ARIMA모델에서 다음으로 고려해야 할 것은 “계절성(Seasonality)”이다. 계절성이란, 일정주기로 특정한 패턴을 보이는 시계열을 예측할때 쓰인다.ARIMA(p,d,q)는 계절내의 모형이 된다. 이와 별도로 계절간 모형을 파악해야 한다. 이때 중요한 것은 계절주기이다. 예를들어, 전력수요는 매월 비슷한주기의 패턴을 보인다. 이 경우 계절주기는 “12”이다. 이러한 같은 계절 끼리 차분한 모형을 “계절차분”라 한다. 아래의 식을 살펴보자.
\[계절간\; 모형: z_1*z_{13}*\dots z_{1+12n}\\ \Phi(B)*\bigtriangledown^{d}_{12}(B)=\epsilon_t*\theta(B)\\\]이때 쓰이는 함수가 자기상관함수(ACF,Auto-Correlation Function)와 편자기상관함수이다.ACF는 현재의 변수가 얼만큼 과거의 변수와 유의미한 상관관계를 갖는지 파악하는 함수이다. ACF가 시작인 k시점에서 t시점까지 모든 변수의 상관관계를 구한다면, PACF는 가장 최초시점인 t시점부터 끝시점인 k시점 중 중간변수의 상관관계를 제거한 변수를 의미한다.
\[per ACF:\rho(k)=Corr(Y_t,Y_{t-k}) \\ =\frac{\displaystyle\sum_{z=k+1}^{t}(Y_t-\bar{Y})(Y_{z-k}-\bar{Y}))}{\displaystyle\sum_{z=k+1}^{t}(Y_t-\bar{Y})} \\ \\ PACF: Corr(Y_t,Y_{t-k}|Y_{t-1},\dots,Y_{t-k+1})\\ * 식은\;생략\]정상적인 시계열이라면 아래와 같은 특징을 지닌다.
-
AR모형일 경우 ACF는 처음 상관계수가 높다가 서서히 줄어든다. 자기상관계수니까 과거값 일수록 상관관계가 적어지는 것은 어찌보면 당연하다.
-
MA모형일 경우 ACF는 k시점 이후 완전히 감소한다. 이동평균은 k시점 이후는 고려하지 않기 때문이다.
-
AR모형일 경우 PACF는 k시점 이후 완전히 감소한다.
-
MA모형일 경우 PACF는 처음 상관계수가 높다가 서서히 줄어든다.

이러한 특징을 통해서 ARIMA계수의 p,d,q를 파악해볼수 있다.아래의 월별전력수요 ACF는 전혀 정상성을 만족하지 못한다. 1회 차분을 한 그래프를 보면 완벽하지 않지만, 정상성을 만족한다. 
ARIMA를 통한 월간전력수요 예측
이제 본격적으로 월간전력수요를 예측해보겠다. 전력수요는 월별 계절성이 있는 시계열이다.ARIMA(p,d,q)(P,D,Q)12의 모형이다. 여기서 계절내/계절간의 AR계수,MA계수, 차분계수를 파악하면 된다.
앞서 이야기한,ACF,PACF함수를 통해서 ARIMA계수를 예측할 수 있지만, R에서는 auto.arima함수를 통해서 최적의 계수를 자동으로 도출할 수 있다. 위 방법이 최선은 아니지만, 본글에서는 위방법을 토대로 진행하겠다.
## Series: ts.elec
## ARIMA(2,1,3)(0,1,2)[12]
##
## Coefficients:
## ar1 ar2 ma1 ma2 ma3 sma1 sma2
## 0.8027 -0.8874 -1.3607 1.3350 -0.5887 -0.6935 0.1092
## s.e. 0.0582 0.0466 0.0499 0.0682 0.0519 0.0458 0.0462
##
## sigma^2 estimated as 933970: log likelihood=-5364.84
## AIC=10745.67 AICc=10745.9 BIC=10781.45
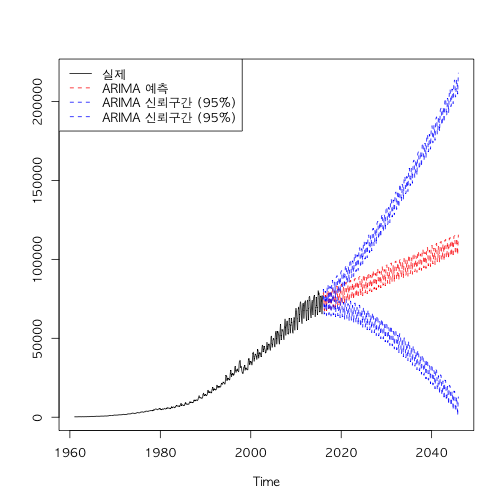
auto.arima를 통해서 도출된 ARIMA모델은 “ARIMA(2,1,3)(0,1,2)[12]”이다. 위 모델을 가지고 향후 30년 전력수요 예측을 95%로 예측하면 아래와 같다.
마무리를 하며
본 예측은 지나치게 긴 기간을 표본(55년)으로 지나치게 긴 기간을 예측(30년)하려고 하여서 유의미한 결과를 도출했다고 보기 어렵다. 차후 예측에는 보다 적은 표본데이터로 적은 기간을 예측해보겠다.