다변량 정규분포
티스토리 블로거 R프렌드님의 포스팅을 토대로 다변량 정규분포에 대해서 살펴보겠다.고등학교때 배운 정규분포는 1개의 변수를 가진다. 트럼프가 선거에서 이길확률과 같이, 단일변수를 가지고 정규분포를 그리며, 모수를 추정한다. 하지만, 때로는 여러가지의 변수를 가지고 확률을 추론 및 분석해야 할 수가 있다.이때 쓰이는 것이 다변량 정규분포이다. 다변량 정규분포에서는 확률 변수 X는 세부 확률변수 $X_1 \dots X_n$을 갖고 이 확률변수는 각각이 하나의 확률분포를 갖는다.
\[X=[X_1,X_2,\dots X_t]\\ X_1 \sim N(\mu_{X1},\sigma^{X_1}),X_2=\dots\]예를 들어보자, 전력가격을 예측하기 위해서는 유가와 발전비중이 중요하다. 유가와 발전비중이 세부 확률변수$X_1$,$X_2$가 될수 있다. 유가와 발전비중은 고정된 변수가 아닌 가각의 확률변수이다. 다변량 확률분포에서는 평균은 벡터로, 공분산은 행렬로 표현된다.
\[E(X)=\begin{bmatrix} E(X_{t}) \\ \vdots \\E(X_{t-s}) \end{bmatrix} =\begin{bmatrix} \mu_{t} \\ \vdots \\\mu_{t-s}\end{bmatrix}=\mu \\ Cov(Y)=\Sigma =E(Y-\mu)(Y-\mu)\\ =E\begin{bmatrix}\begin{pmatrix} Y_{t}-\mu_t \\ \vdots \\Y_{t-s}-\mu_{t-s}\end{pmatrix} \begin{pmatrix}Y_{t}-\mu_t, \dots,Y_{t-s}-\mu_{t-s}\end{pmatrix} \end{bmatrix}\]다변량 정규분포의 정규분포 확률분포식은 아래와 같다. (당연히 증명을 할 줄을 모른다;;) 여기서 $\Sigma$는 공분산행렬을 의미한다.
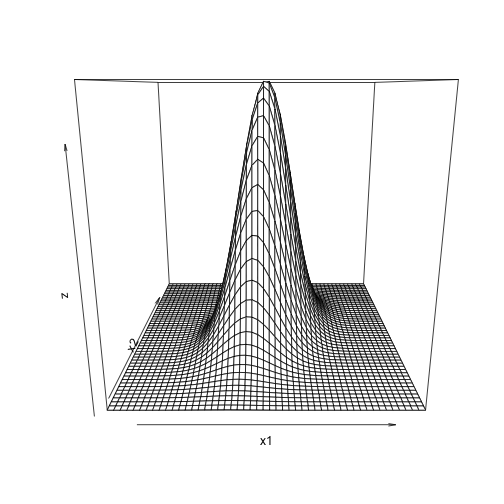
\[f(x)=\frac{1}{\sqrt{(2\pi)^{n/2}|\boldsymbol\Sigma|^{1/2}}} \exp\left(-\frac{1}{2}({x}-{\mu})^T{\boldsymbol\Sigma}^{-1}({x}-{\mu}) \right)\]2변량 변수 정규분포 그리기
을 토대로 다변량 정규분포를 한번 그려보겠다. 우리가 직관적으로 볼 수있는 함수는 3차원이므로, 세부확률변수가 2개이고, 표준정규분포를 따른다고 가정을 하겠다.